Sinkhorn divergence gradient flows

Let \(\mathrm{OT_\varepsilon}(\alpha, \beta)\) the entropic regularized OT distance between two distributions \(\alpha\) and \(\beta\). One issue with \(\mathrm{OT_\varepsilon}\) is that \(\mathrm{OT_\varepsilon}(\alpha, \alpha)\) is not equal to 0.

The Sinkhorn divergence, defined in [Genevay et al., 2018] as \(\mathrm{S}_\varepsilon(\alpha, \beta) = \mathrm{OT_\varepsilon}(\alpha, \beta) - \frac{1}{2}\mathrm{OT_\varepsilon}(\alpha, \alpha) - \frac{1}{2}\mathrm{OT_\varepsilon}(\beta, \beta)\) removes this entropic bias.

In this tutorial we showcase the advantage of removing the entropic bias using gradient flows on 2-D distributions, as done in [Feydy et al., 2019] and following the Point Clouds tutorial.

Imports

import sys

if "google.colab" in sys.modules:
    !pip install -q git+https://github.com/ott-jax/ott@main

from typing import Any, Callable, Tuple

import jax
import jax.numpy as jnp

import matplotlib.pyplot as plt
from IPython import display

import ott
from ott.geometry import pointcloud
from ott.problems.linear import linear_problem
from ott.solvers.linear import sinkhorn
from ott.tools import plot, sinkhorn_divergence

Sampling Source/Target Distributions

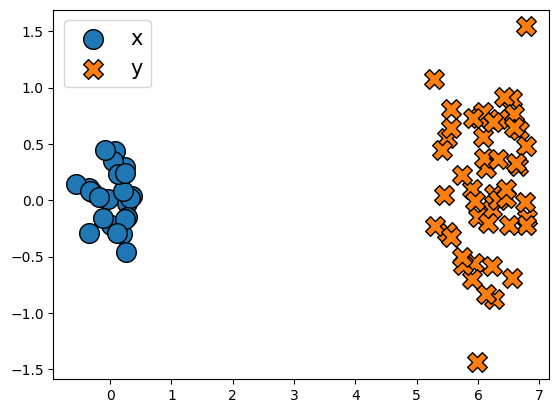
Let us start by defining simple source and target distributions.

key1, key2 = jax.random.split(jax.random.PRNGKey(0), 2)

x = 0.25 * jax.random.normal(key1, (25, 2))  # Source
y = 0.5 * jax.random.normal(key2, (50, 2)) + jnp.array((6, 0))  # Target

plt.scatter(x[:, 0], x[:, 1], edgecolors="k", marker="o", label="x", s=200)
plt.scatter(y[:, 0], y[:, 1], edgecolors="k", marker="X", label="y", s=200)
plt.legend(fontsize=15)
plt.show()

Gradient Flow of a Divergence

The code below performs gradient descent to move points in a point cloud x in a way that minimizes a divergence to another point cloud y, divergence(x, y, epsilon).

def gradient_flow(
    x: jnp.ndarray,
    y: jnp.ndarray,
    divergence: Callable[[jnp.ndarray, jnp.ndarray, float], Tuple[float, Any]],
    num_iter: int = 500,
    lr: float = 0.2,
    dump_every: int = 50,
    epsilon: float = None,
):
    """Compute an entropic Wasserstein (possibly debiased) gradient flow."""

    ots = []

    # Apply jax.value_and_grad operator and jit that function.
    divergence_vg = jax.jit(jax.value_and_grad(divergence, has_aux=True))

    # Perform gradient descent on `x`.
    for i in range(0, num_iter + 1):
        (cost, ot), grad_x = divergence_vg(x, y, epsilon)
        assert ot.converged
        x = x - grad_x * lr  # Perform a gradient descent step.
        if i % dump_every == 0:
            ots.append(ot)  # Save the current state of the optimization.

    return ots

def display_animation(ots, plot_class=plot.Plot):
    """Display an animation of the gradient flow."""
    plott = plot_class(show_lines=False)
    anim = plott.animate(ots, frame_rate=4)
    html = display.HTML(anim.to_jshtml())
    display.display(html)
    plt.close()

Gradient Flow of \(\mathrm{OT}_\varepsilon\)

We set the divergence to be the regularized OT cost.

def reg_ot_cost(x, y, epsilon=None):
    """Return the OT cost and OT output given a geometry"""
    geom = pointcloud.PointCloud(x, y, epsilon=epsilon)
    ot = sinkhorn.Sinkhorn()(linear_problem.LinearProblem(geom))
    return ot.reg_ot_cost, ot

For the default value of \(\varepsilon\), the gradient flow behaves as expected:

# Compute and display the gradient flow for the regularized OT cost.
ots = gradient_flow(x, y, reg_ot_cost)
display_animation(ots)

Once Loop Reflect

But for a larger \(\varepsilon\), the distribution collapses:

# Compute and display the gradient flow for a larger value of epsilon.
ots = gradient_flow(x, y, reg_ot_cost, epsilon=1.0)
display_animation(ots)

Once Loop Reflect

This is expected: the regularized OT plan collapses to a rank \(1\) matrix (here the matrix of ones divided by \(nm\)) and simply leads all points in \(x\) to the mean of points in \(y\).

Let us fix this by choosing for the divergence the debiased Sinkhorn divergence, \(\mathrm{S}_\varepsilon\).

Gradient flow with \(\mathrm{S}_\varepsilon\)

By slightly adapting the previous function, we can compute the gradient flow using the sinkhorn_divergence() instead of the regularized OT cost.

def sink_div(x, y, epsilon=None):
    """Return the Sinkhorn divergence cost and OT output given point clouds.

    Since ``y`` is fixed, we can use the flag ``static_b=True`` to avoid
    computing the ``reg_ot_cost(y, y)`` term.
    """
    ot = sinkhorn_divergence.sinkhorn_divergence(
        pointcloud.PointCloud,
        x=x,
        y=y,
        epsilon=epsilon,
        static_b=True,
    )
    return ot.divergence, ot

We also have to adapt the plotting object slightly to deal with the fact that we have Sinkhorn divergence outputs, which have multiple geometries.

class CustomPlot(plot.Plot):
    def _scatter(self, ot):
        x, y = ot.geoms[0].x, ot.geoms[0].y
        a, b = ot.a, ot.b
        scales_x = a * self._scale * a.shape[0]
        scales_y = b * self._scale * b.shape[0]
        return x, y, scales_x, scales_y

Thanks to the debiasing, the distributions overlap nicely, even for a large \(\varepsilon\).

# Compute and display the sinkhorn divergence gradient flow for the same large epsilon.
ots = gradient_flow(x, y, sink_div, epsilon=1.0)
display_animation(ots, plot_class=CustomPlot)

Once Loop Reflect